Mathematics-Inspired Glass Sculptures
Bronna designs and fabricates glass sculptures by cutting the glass, painting imagery on it with vitreous paints and silver stains, firing it in a kiln, and assembling the pieces, often with stainless steel and/or wooden bases, sometimes with electronics. The piece to the left, “What Time Is It?” is a puzzle that can only be solved when three people work together.
Mathematicians Jayadev Athreya,
David Aulicino and Patrick Hooper
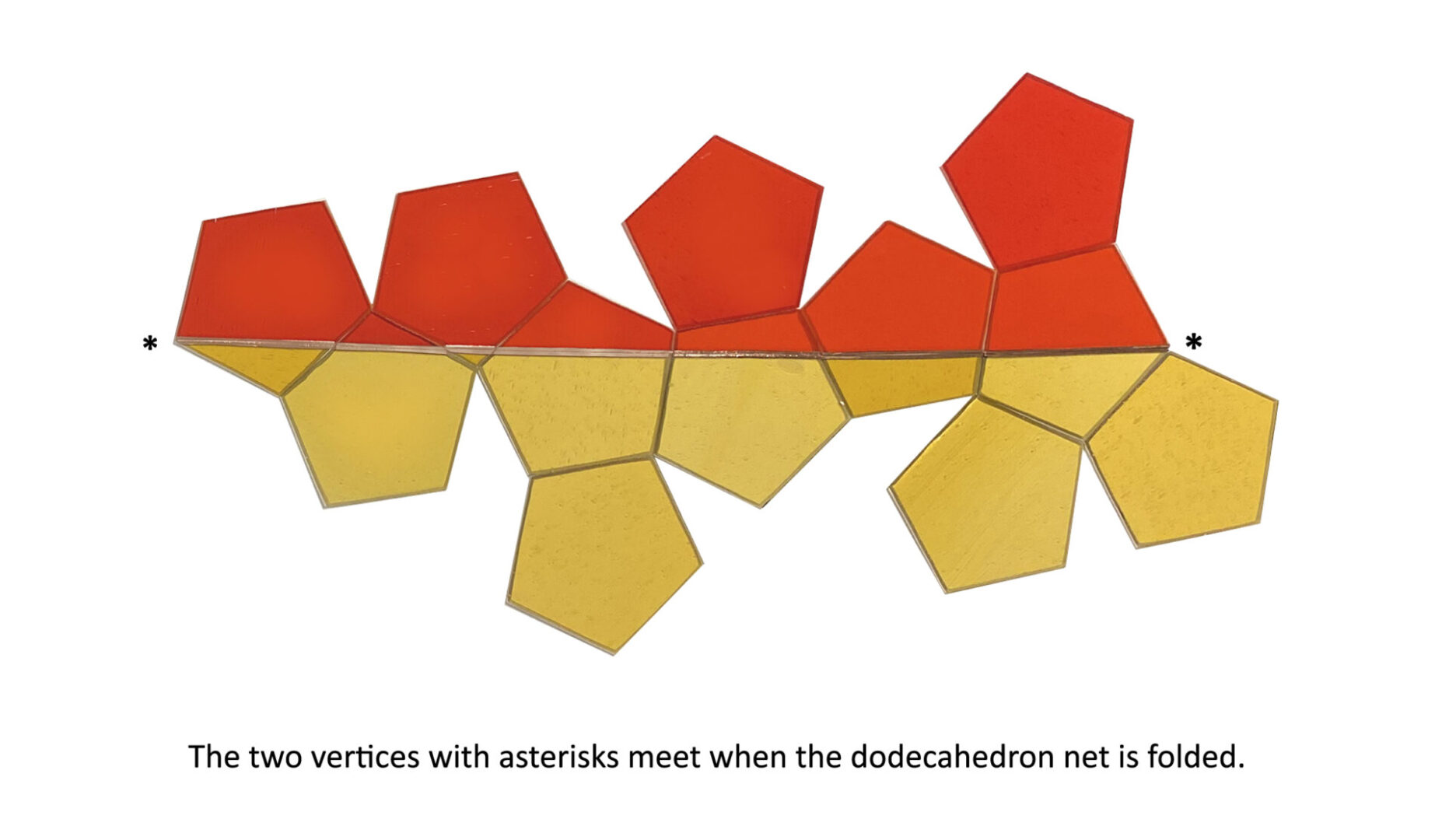
Recently proved that there are an infinite number of straight paths on the dodecahedron that start at one vertex, proceed in a straight path around the Platonic solid, returning to the starting vertex without passing through any other vertices. Mathematician Ingrid Daubechies introduced Bronna to this breakthrough during their collaboration on the installation, Mathemalchemy. Bronna illustrated one of these straight paths on the stained-glass dodecahedron that she created for the installation’s lighthouse, which will be lit.
The solution to the stained-glass cuboctahedron puzzle, “Persistence/Teamwork”, is the identity of a significant date, which is the 100-year anniversary of the confirmation of a major theory of physics.
The puzzle requires three participants to solve the puzzle. Each participant can only see the variables/numbers that are above his/her dial. A unique set of three numbers for the F, G and H variables is generated when the dials are pressed. The values are used in three equations painted on the glass. After solving the equations, each player can enter one of the numbers for D, M or Y. When the correct date has been entered, the puzzle will light a clue to the significant date.
Persistence/Teamwork was a collaboration by puzzle-meister and escape-room-builder Brett Kuehner, analytical chemist techie Michael Ribick and artist Bronna Butler. It was created to highlight the importance of persistence in the study of mathematics and the value of collaborating with other individuals.
A laser beam fired through a certain type of crystal can cause individual photons, at the quantum level, to be split into pairs of entangled photons....actions performed on one affect the other, even when they are separated by great distances.
My piece, "Entangled", depicts two sets of entangled particles. I painted (and fired in a kiln) 2D de Bruijn 4 X 4 arrays (window length four) on two clear glass panels, with spinning red and yellow particles in the same 2 X 2 windows - separated by the space between the panels. For one of the “like-colored” pairs, one of the photons has been "observed/measured."
From the observation of the sets of painted particles, a viewer can determine which of the two painted pairs has been "measured". The 28 X 30 X 30 cm painted glass, stainless steel, and wood piece was completed in 2018.
A (double) null cone depiction/drawing of space-time in Roger Penrose’s recent book, Fashion Faith and Fantasy in the New Physics of the Universe, inspired my piece “The Future of 11 in Space-time.”
“A null/light cone is the path that a flash of light, emanating from a single event (localized to a single point in space and a single moment in time) and traveling in all directions, would take through spacetime.”
One of the double cones is the future null cone, the other is the past null cone. Using five, consecutive transparent glass panels to suggest the passage of time, I depicted the double-null-cone-image on its side, so the viewer is looking “into” the cones. I painted “slices” of an implied swirling-cone-interior on the glass panels, using vitreous paints, and fired them in a kiln.
“1011,” binary code for the decimal number 11, is painted in red on each of the outer-most transparent panels. “1101,” binary code for the decimal number 13 (the mirror image of 1011 for 11) can be seen, through the transparent panels, on the backside of the back panel (viewed from either side).
The 1011 and 1101 digits “swirl” down into, and out of, the two cones, the past and the future. For my piece, the future of 11 in space-time is 13 (the consecutive prime number). The 28 X 31 X 24 cm painted glass and stainless-steel piece was completed in 2018.
I collaborated with John Horton Conway on this stained glass, multifaceted portrait of him.
The 14 X 18 X 18 in. sculpture is primarily a depiction of Conway's Cosmogram, which I fabricated in stained glass. The various inscriptions of the Platonic solids in each other are all visible in the Cosmogram.
I designed, painted, and fired images on some of the glass pieces, including a portrait of Conway, one of his quotes and another quote about him, his signature, the ratios of the edges and volumes of the Platonic solids inscribed, and several of Kepler's great stellated dodecahedra from his "Harmonices Mundi." Conway was Princeton’s John von Neuman Professor.
Conway has, on many occasions, offered a minor financial incentive/reward to any of his math colleagues who could find a solution to a difficult mathematical problem.
This inspired me to create a 5 X 6 X 6 in. stained glass pyramid with a challenge/puzzle painted on three of its sides, and the words "$50 if you can figure out the pattern" on one side. (The puzzle pattern has been circulating among groups of mathematicians for years. It is in Conway's biography, "Genius at Play", by Siobhan Roberts). A $50 bill is inside the pyramid to complete the playful reference.
Any piece about the prolific Martin Gardener (1914-2010) carries a genuine responsibility to honor this remarkable person. He is beloved by mathematicians, magicians, puzzlers, and rational skeptics, as well as “lay” and professional math and science enthusiasts throughout the world.
Gardner published over 70 books covering subjects from literature, such as The Annotated Alice (Alice’s Adventures in Wonderland and Through the Looking Glass), to Magic, Skepticism, Religion, and fictional novels. For 25 years, Martin wrote the “Mathematical Games” column for Scientific American magazine.
It was the magazine’s most popular column ever. I have run into Gardner enthusiasts many times who, at the mention of his name, begin to glow with enthusiasm and gush personal stories of Gardner’s influence in their lives. My favorite quote about Gardner was written by Persi Diaconis, “Warning: Martin Gardner has turned dozens of innocent youngsters into math professors and thousands of math professors into innocent youngsters.”
Using Gardner’s autobiography, Undiluted Hocus-Pocus, his numerous columns and books, and conversations with individuals who knew him, I have included a number of references to his life in this “multi-faceted” portrait….such as hexaflexagons, encoded words, “Alice” imagery and rainbow colors captured in glass (the two pocket watches are set to 2:10).
This glass portrait-sculpture is 11 X 12 X 9 inches. Three of the preliminary 18 X 24-inch drawings are shown below. Did I capture Martin Gardner in a compact portrait? Not possible. Quoting renowned mathematician, and Gardner’s personal friend, John Horton Conway, “Martin Gardner was the most learned man I have ever met. He wrote articles and books for mathematicians, magicians, and puzzle lovers. And he didn’t even get quantum mechanics wrong!”
"Reflected tessellation" includes two clear panes of glass on which I painted (and fired in a kiln) my tile design of fish.
In order to suggest additional dimension to the tiles, I painted the green fish on the front of the glass, and the alternating bluefish on the back of the 1/8-inch-thick glass. The two panes of fish were also meant to add dimension.
One of the fish on the front panel appears to be “breaking away” from the “pack”. Three glass cuboids, painted with fish and a puzzle, surround the glass panes. There are five reflecting surfaces, in which the images of the transparent, painted fish can be seen. The puzzle text asks: "Number of reflected fish minus glassfish equals.....?" An observant individual will not need to add the reflected fish. The answer contains a non-number symbol. The 30 X 30 X 24 cm painted glass and stainless-steel piece was completed in 2018.
The multifaceted portrait of John Nash includes references to his work, for which he won both Nobel and Abel prizes.
Images of Nash and his wife, Alicia, a quote from Nash, his signature and some of his notes, along with many other references to his life are also included. The mirrored pyramid, inside the 8.5 in. stained glass cube, directs the light throughout the glass. The reflections in the pyramid create four different "floors" in the portrait, depending on the viewer's angle of sight.
The 8.5 in. cube multifaceted portrait of Dr. Richard Feynman includes some of Feynman's diagrams, achievements, three quotes, “O-ring” feet, and other images from his life, including scenes from Tuva.
Feynman would sometimes use Tuva, the geographic center of Asia, to inspire his students and others to reach for, and discover new things. Travel to Tuva was a long time goal for Feynman, which was not realized. Scenes of Tuva are painted on four interior panels of the multifaceted cube. If an observer looks down through the top of the cube, where Feynman's portrait is painted, the mirror at the bottom reflects Feynman's image in the center of the Tuva images.
The three-paneled glass portrait of actor Reginald L. Barnes
Includes several of his quotes, painted on glass and assembled in front of mirrors, and multiple images of his family and him.
Angelic Aunt Hazel is painted on three layers of antique clear glass.